В гидравлических закрытых подсистемах влиянием высоты столба жидкости на давление можно пренебречь, так как рабочее давление существенно превышают те, которые обусловлены высотой столба жидкости.

Переменной типа потока является объемный расход G, переменной типа потенциала давление P.

Простейшие элементы: потеря давления R, сжимаемость Cg, инерционность Lg, компонентные уравнения которых:

G=P, G=C_g, P=L_g

и источники расхода и давления с компонентными уравнениями

G=G(Z), P=P(Z),

где в качестве Z может фигурировать время или фазовая переменная.

Получить компонентные уравнения простейших элементов можно следующим образом. Потери давления в трубопроводе при стационарном ламинарном течении жидкости оцениваются с помощью формулы Пуазейля:

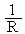
P=128G , или G=P, где R= 128,

ν - кинематическая вязкость жидкости, ρ - ее плотность, l - длина, d - диаметр трубопровода.

Уравнение элемента сжимаемости (гидравлической емкости) может быть получено из определения коэффициента сжимаемости

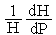
β = , где H - объем жидкости, P - давление. Выполним следующие преобразования:

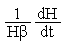
= , или G=C_g , где Cg = Hβ.

В тех случаях, когда удобнее в математических моделях использовать модуль упругости жидкости, уравнение элемента сжимаемости может быть получено из уравнения закона Гука. Предположим жидкость сжимается в цилиндрическом сосуде с площадью поперечного сечения S и высотой столба жидкости l. Согласно закону Гука = , где E - модуль упругости жидкости, Δl - изменение высоты столба жидкости под давлением P. Продифференцировав по времени и умножив обе части уравнения на S, получим

= SV= G=,

где V скорость перемещения верхней границы жидкости под давлением, Н - объем жидкости

Для модуля упругости рабочих жидкостей в литературе проводятся зависимости от температуры и газосодержания которые могут быть использованы при реализации моделей в программно-методических комплексах моделирования.

Уравнение элемента инерционности можно получить из уравнения Ньютона для массы жидкости m, движущейся по участку трубопровода длиной l и площадью поперечного сечения S со скоростью V: F=m . Выполним преобразования для перехода к фазовым переменным G и P.

PS=ρlS P= P=L_g, где L_g=

Условные изображения элементов на эквивалентных схемах представлены на рис.2.8

1. Базовый узел эквивалентной схемы соответствует точке отсчета давления - либо абсолютному нулю, либо атмосферному давлению. Выбор точки отсчета зависит от реализованных в математических моделях зависимостях, например зависимости модуля упругости от газосодержания и температуры.

2. В подсистеме выделяются элементы, сжимаемость жидкости в которых оказывает существенное влияние на динамику подсистемы, как правило это резервуары значительного объема. На эквивалентных схемах такие элементы одним полюсом подключаются к базовому узлу. Все взаимодействия с окружающей средой осуществляются через второй полюс.

3. В гидравлических подсистемах, кроме резервуаров, из пассивных элементов присутствуют дроссели и трубопроводы. Они включаются между соответствующими резервуарами или между собой. Трубопровод, в тех случаях, когда можно пренебречь волновыми процессами, отображается элементом потерь или последовательно включенными элементом потерь и элементом инерционности, в противном случае необходимо использовать более сложные модели, например модели с распределенными параметрами.

4. Активные компоненты - насосы, аккумуляторы давления отображаются на эквивалентных схемах в виде источников расхода и давления ограниченной мощности.

Пример эквивалентной схемы для гидравлической подсистемы (рис.2) представлен на рис.3.

На эквивалентной схеме дроссели Д1-Д3 представлены элементами потери давления R1-R3, трубопроводы от насоса Н к резервуарам С1-С3 элементами R4-R6.