Типы связей между подсистемами можно классифицировать следующим образом:

1) трансформаторный

2) гираторный

3) через зависимые параметры

4) дифференциальный

5)интегральный

Эквивалентная схема этого типа связи представлена на рис.1

Рассмотрим эквивалентную схему объекта(рис.3), представленного на рис.2

Здесь источники V₁ и M₁ представляют трансформаторное взаимодействие поступательной подсистемы с массой m1 и вращательной, а источники V₂ и M₂ - взаимодействие поступательной подсистемы с массой m2 и вращательной.

Для этого типа можно предложить два равноценных варианта эквивалентных схем, которые отличаются использованием зависимых источников различных типов - потока (рис.4)или потенциала (рис.5).

Учитывая особенности методов формирования ММС предпочтение следует отдать первой схеме ( рис.4).

. Рассмотрим этот вид взаимодействия при построении эквивалентной схемы простейшего одностороннего гидроцилиндра (рис.6). Предполагая, что корпус цилиндра неподвижен, можно построить эквивалентную схему, показанную на рис.7.

Здесь P - источник внешнего давления на входе в трубопровод, Rg и Lg - потери и инерция движения жидкости в трубопроводе, Сg - полость гидроцилиндра, М - масса поршня, TR1 - трение поршня о стенки, U1 - упругость штока от поршня до стенки, U2 - упругость остальной части штока, F2 - внешнее воздействие на шток. Источники G и F - элементы гираторной связи с компонентными уравнениями G=V*S и F=P_c*S, где S -площадь поперечного сечения поршня, V - скорость движения поршня, P_c - давление в гидроцилиндре.

Эквивалентная схема этого типа связи представлена на рис.8

В подсистеме Р размещается элемент, параметры которого зависят от фазовых переменных подсистемы Q, в подсистеме Q - источник переменной типа потока, зависящий от фазовых переменных подсистемы Р. Примером такого взаимодействия может служить взаимодействие гиравлической и тепловой подсистем. Вязкость рабочих жидкостей в гидравлике существенным образом зависит от температуры, гидравлические потери, то есть тепловыделение - от вязкости.

Рассмотрим простейшую гидросистему (рис.9), состоящую из последовательно включенных насоса(Н), дросселя(D) и бака(Б).

При составлении эквивалентной схемы будем пренебрегать потерями в трубопроводе. Эквивалентная схема установки при совместном моделировании гидравлических и тепловых процессов представлена на рис.10

Здесь G- расход, подаваемый насосом, R- гидросопротивление дросселя, С1-С3 - теплоемкости насоса, дросселя и бака соответственно, R1-R3 - конвекционные сопротивления для этих же элементов, Тк- источник температуры, равный температуре окружающей среды. Элементы Ф1,Ф2 - источники теплового потока, обусловленные потерями в насосе и дросселе с компонентными уравнениями:

Ф1=Р_нG_н(1-η), Ф2=Р_дG_д,

здесь Р_н- давление, создаваемое насосом, G_н- подача (расход) насоса, η-КПД насоса, Р_д- перепад давления на дросселе, G_д- расход через него. Ф3-Ф5 -тепловые потоки, обусловленные массопереносом, с компонентными уравнениями:

Ф3=С_тρТ_нG, Ф4=С_тρТ_дG, Ф5=С_тρТ_бG,

здесь С_т - удельная теплоемкость жидкости, ρ-ее плотность, G -расход, Т_н,Т_д и Т_б - температуры насоса, дросселя и бака соответственно. Компонентные уравнения тепловых потоков, обусловленных массопереносом, получены следующим образом. Количество теплоты, запасенное в жидкости, определяется уравнением:

Q= CтmT=CтρVT, где V- объем жидкости. продифференцировав по времени и учитывая, что , получим Ф=СтρGT.

Таким образом, влияние гидравлической подсистемы на тепловую учитывается введением источников теплового потока, обратное влияние - зависимостью параметров гидравлической подсистемы ( в первую очередь коэффициента вязкости жидкости) от температуры.

Эквивалентная схема этого вида связи представлена на рис.11

Примером такого типа взаимодействия может служить взаимовлияние магнитной и электрической подсистем.

Рассмотрим построение эквивалентной схемы трехобмоточного трансформатора с зазором в магнитопроводе (рис.12).

На эквивалентной схеме (рис.13) электрическая подсистема представлена элементами R1-R3, являющимися активными сопротивлениями обмоток и элементами E1-E3, учитывающими влияние магнитной подсистемы на электрическую, их компонентные уравнения имеют вид:

E1=W₁ , E2=W₂ , E3=W₃ ,

где W_i- количество витков i-ой обмотки, Ф_i- магнитный поток, пронизывающий i-ю обмотку.

Магнитная подсистема представлена элементами R_М1-R_М7 - являющимися магнитными сопротивлениями участков магнитопровода l₁-l₇, R_Z1-R_Z3 - магнитными сопротивлениями соответствующих зазоров, тремя дифференциаторами, необходимыми для получения производных dФ_i/dt и трех источников магнитного напряжения U_M1-U_M3, учитывающих влияние электрических подсистем на магнитную, с компонентными уравнениями:

U_M1=I₁W₁, U_M2=I₂W₂, U_M3=I₃W₃.

Эквивалентная схема этого типа связи приведена на рис.14

В подсистеме Р размещается элемент, параметр которого зависит от интеграла фазовой переменной их подсистемы Q, в подсистеме Q - исочник, зависящий от фазовой переменной подсистемы Р.

Рассмотрим взаимодействие магнитной и механической поступательной подсистем на примере электромагнитного реле схематично изображенного на рис.15

В следствие малости зазора между перемычкой П и магнитопроводом будем считать ее перемещение поступательным. Работа по перемещению перемычки П осуществляется за счет изменения энергии магнитного поля в зазоре X. Значение силы, действующей на перемычку, может быть получено из выражения:

F= ,

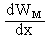
где W_M - энергия магнитного поля, которая в общем случае может быть вычислена по формуле:

W_M=∫dV,

здесь V- объем, в котором рассчитывается энергия. В нашем случае, считая, что поле в зазоре однородно, а площадь поперечного сечения зазора S, получим:

W_M =xS, или F==S=S=

.

Таким образом, сила, действующая на перемычку П, зависит от магнитного потока Ф, а магнитный поток зависит от сопротивления цепи, в рассматриваемом случае от величины зазора. На основании этого можно предложить эквивалентную схему для учета взаимовлияния механической поступательной и магнитной подсистем (рис.16)

Магнитная подсистема представлена магнитным сопротивлением, зависящим от величины зазора, и имеющим компонентное уравнение :

.R_M=

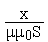
Механическая поступательная подсистема представлена источником силы, являющимся функцией магнитного потока Ф, с компонентным уравнением:

F=

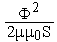
и интегратором, состоящим из элементов I и C, позволяющим получать в качестве фазовой переменной перемещение x.

Полная эквивалентная схема реле, с учетом взаимодействия электрической, магнитной и механической подсистем, представлена на рис.17.

Здесь Е1 - источник напряжения, запитывающий реле, R1 - сопротивление обмотки; Е2 - источник, учитывающий влияние магнитной подсистемы на электрическую; E3 - источник магнитного напряжения, учитывающий влияние электрической подсистемы на магнитную; Rм - магнитное сопротивление магнитопровода; Rz - переменное сопротивление зазора между сердечником и якорем, это сопротивление учитывает влияние механической подсистемы на магнитную; F1 - источник силы, учитывающий влияние магнитной подсистемы на механическую; F2 - источник силы, моделирующий предварительное поджатие контактной группы; m - масса якоря; С1 - жесткость контактов, С2 - нелинейная жесткость, моделирующая двусторонний упор при перемещении якоря; R2 - приведенное трение; элементы I1,L образуют дифференциатор для получения dФ/dt, присутствующего в компонентном уравнении Е2; элементы I2,C образуют интегратор